Additionneur non-inverseur
Imprimer cette page
Fiche récapitulative du montage additionneur non-inverseur
a) schéma
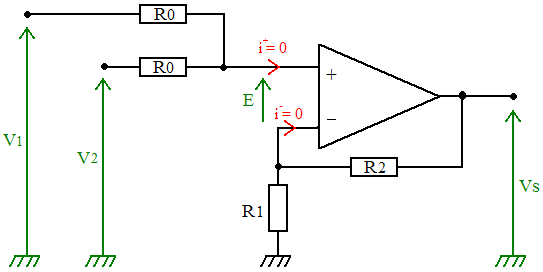
b) formule
OU :
c) Remarques
A partir de ce schéma on peut rajouter autant de tension d'entrées que nécessaire (à condition de rajoutez autant de résistance R0). C'est ainsi un montage additionneur non-inverseur extensible à n entrées.
La résistance de chaque entrée vaut au moins R1.
Comment calculer Vs en fonction de Ve
Pour ce calcul, on va considérer un montage additionneur non-inverseur avec 2 entrées (V1 et V2)
Comme pour d'autres montages de l'AOP, nous pouvons dire qu'avec cet additionneur non-inverseur on a:
- Un fonctionnement linéaire
- Un AOP supposé parfait, donc E=0V, ainsi V+=V-
Alors, pour déterminer Vs de l'additinneur non-inverseur il faut déterminer V+ et V- de l'équation V+=V-:
- Calcul de V+: A l'aide du théorème de Millman on peut en déduire cette formule:
=>
=>
- Calcul de V-: A l'aide du diviseur de tension on peut déduire cette formule:
Sachant que V+=V-, on a:
Il est judicieux maintenant d'isoler Vs de l'additionneur non-inverseur:
=>
Nous avons ainsi déterminer la formule de l'additionneur non-inverseur à 2 entrées. Pour n entrées nous aurions eu cette formule:
Le montage porte le nom d'additionneur non-inverseur car il additionne les tensions d'entrées sans les inverser.
N'hésitez pas à consulter les autres montages de base de l'amplificateur opérationnel (AOP)
Flux RSS